![]() can be triangulated into eight triangular regions. This triangulation has the same symmetry group as the octahedron. The triangulation basically consists of connecting the six points
can be triangulated into eight triangular regions. This triangulation has the same symmetry group as the octahedron. The triangulation basically consists of connecting the six points
![]() ,
,
![]() ,
,
![]() with great circles in the x-y, y-z and z-x planes. Cutting the sphere along these lines, and then laying out the eight resulting triangles in a plane can be thought of as another visualization technique for two-dimensional beings.
with great circles in the x-y, y-z and z-x planes. Cutting the sphere along these lines, and then laying out the eight resulting triangles in a plane can be thought of as another visualization technique for two-dimensional beings.
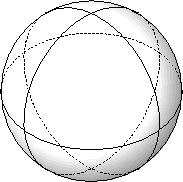
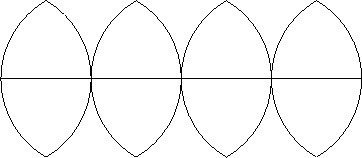
Similarly,
![]() can be triangulated into sixteen tetrahedral regions by connecting the eight points
can be triangulated into sixteen tetrahedral regions by connecting the eight points
![]() ,
,
![]() ,
,
![]() ,
,
![]() with great spheres. This triangulation has the same symmetry as the sixteen-cell polytope. Like the triangulation of
with great spheres. This triangulation has the same symmetry as the sixteen-cell polytope. Like the triangulation of
![]() , this can be used as another method of visualization of
, this can be used as another method of visualization of
![]() , and it will be, later.
, and it will be, later.
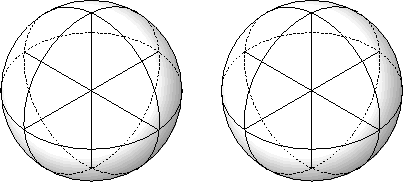
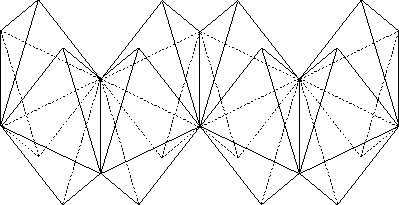
Notice that there are a great many more possibilities for how these sixteen tetrahedra can be arranged than there are for the triangulation of
![]() . Might there be a particularly orderly arrangement for them, that had no analogue in
. Might there be a particularly orderly arrangement for them, that had no analogue in
![]() ?
?
Since an analogue of the symmetry group of the octahedron and the sixteen-cell exists in every dimension, we can generalize this process of triangulation to
![]() , decomposing it into
, decomposing it into ![]() n-cells.
n-cells.