Surgery on knots is the process of embedding a knot inside a manifold, removing a tubular neighborhood of the knot from the manifold, and then re-gluing it to the manifold in a different fashion. Although it might not seem possible, different manifolds can be created in the process. For the purposes of this paper, I will look at one of the simplest of these processes; surgery on the unknot, or circle, in
![]() .
.
When a tubular neighborhood of the unknot is removed from the sphere, and glued back to the sphere in a different fashion, the resulting manifold is
![]() . This is not an easy fact to see.
. This is not an easy fact to see.
First, we must notice that removing a circular neighborhood of the unknot is the same as removing a filled torus. Since we already know that cutting
![]() along the surface of
along the surface of
![]() separates it into two filled tori, we know that removing one filled torus leaves another filled torus. So imagine our sphere is now separated into two identical filled tori.
separates it into two filled tori, we know that removing one filled torus leaves another filled torus. So imagine our sphere is now separated into two identical filled tori.
Now, let's look at the surface of a great sphere, and how it is divided by the two tori. Look again at the picture of the equatorial torus in section 4.1. Consider the great sphere which is flattened into the x-y plane in these images. It is split into three pieces. It passes through one filled torus twice, in two disk-like regions around opposite poles of the great sphere. It passes through the other filled torus in an annular region.
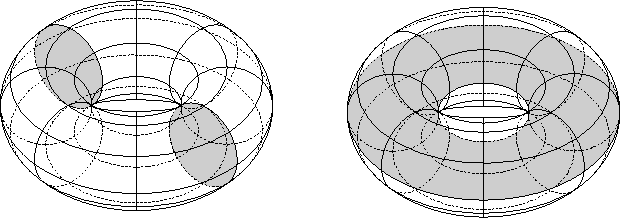
Now if we look at one of our two filled tori, say, the one on the right above, and draw in this annular surface formed by intersection with the great sphere, we can see how it must be glued to the other filled torus. In particular, this annular region must be glued to two disks in the other torus to make a
![]() .
So the two tori are glued with generators swapped; the generator that ``goes around the hole'' in one torus is glued to the generator that ``goes through the hole'' in the other, and vice versa. In other words, the ``tube'' of one torus goes through the ``hole'' of the other.
.
So the two tori are glued with generators swapped; the generator that ``goes around the hole'' in one torus is glued to the generator that ``goes through the hole'' in the other, and vice versa. In other words, the ``tube'' of one torus goes through the ``hole'' of the other.
Now, if we re-glue the tori so that the generators are not swapped, and corresponding points on the tori are glued to each other. then we will get a different manifold. Each boundary of each annular region is glued to the corresponding boundary of the corresponding annular region in the other torus. And each circular region is glued to another circular region, to make a sphere. In other words, at each point on a circle going ``around the hole'' of the torus, there is a sphere formed by gluing two disks that intersects the circle at that point. So, after the surgery, the manifold is no longer
![]() , but instead
, but instead
![]() , another three dimensional manifold that can not be topologically distorted to the sphere.
, another three dimensional manifold that can not be topologically distorted to the sphere.