Two unit circles in
![]() , one in the x-y plane and the other in the z-w plane, form the basis of a curious structure on
, one in the x-y plane and the other in the z-w plane, form the basis of a curious structure on
![]() . The surface of a tubular neighborhood a fixed distance from either of these circles forms a torus in
. The surface of a tubular neighborhood a fixed distance from either of these circles forms a torus in
![]() . The Clifford Tori are the family of tori generated by tubular neighborhoods around either of these centerlines. A tubular neighborhood at a distance of n from one centerline is the tubular neighborhood at a distance of
. The Clifford Tori are the family of tori generated by tubular neighborhoods around either of these centerlines. A tubular neighborhood at a distance of n from one centerline is the tubular neighborhood at a distance of ![]() from the other, where
from the other, where
![]() . The family of tori generated by varying
. The family of tori generated by varying ![]() are called the Clifford Tori. The tubular neighborhood at a distance of
are called the Clifford Tori. The tubular neighborhood at a distance of
![]() forms the flat torus in
forms the flat torus in
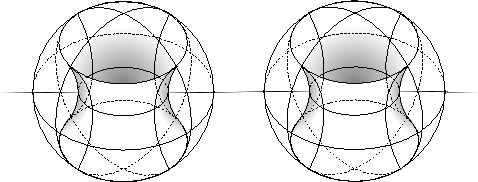
![]() mentioned above. I'll call this torus the equatorial torus, because, like an equator, we shall see that it divides the sphere neatly into two identical pieces.
mentioned above. I'll call this torus the equatorial torus, because, like an equator, we shall see that it divides the sphere neatly into two identical pieces.
It is important to note that
![]() can be embedded in
can be embedded in
![]() so that it is ``flat,'' that is, so that it's Gaussian curvature is 0 at every point. This is not possible in
so that it is ``flat,'' that is, so that it's Gaussian curvature is 0 at every point. This is not possible in
![]() . Additionally, the Clifford Tori are embedded ``flatly'' in
. Additionally, the Clifford Tori are embedded ``flatly'' in
![]() .
.
Not only does
![]() divide
divide
![]() into two filled tori, but this division can be done in a geometrical way. In other words, if we cut the sphere into two pieces along this special torus, we could swap the two pieces (in
into two filled tori, but this division can be done in a geometrical way. In other words, if we cut the sphere into two pieces along this special torus, we could swap the two pieces (in
![]() ) of the
) of the
![]() and rearrange them back into a sphere. This means we might expect it to be possible to ``invert'' or swap these regions in
and rearrange them back into a sphere. This means we might expect it to be possible to ``invert'' or swap these regions in
![]() via isometries. In fact, this is possible. We can swap the two centerlines, (and their tubular neighborhoods along with them) by rotating first by
via isometries. In fact, this is possible. We can swap the two centerlines, (and their tubular neighborhoods along with them) by rotating first by
![]() in the x-z plane, and then by
in the x-z plane, and then by
![]() in the y-w plane.
in the y-w plane.

This operation also makes it possible to see another interesting fact about inverting
![]() in
in
![]() . Since
. Since
![]() , we can distinguish two unique, perpendicular lines on the surface of
, we can distinguish two unique, perpendicular lines on the surface of
![]() (A and B) and call them the generators.
If we choose the generators so that one is in the direction of one of the centerlines, and the other in the direction of the other centerline, and then watch these generators as we rotate the sphere, we can see that they are swapped as well.
(A and B) and call them the generators.
If we choose the generators so that one is in the direction of one of the centerlines, and the other in the direction of the other centerline, and then watch these generators as we rotate the sphere, we can see that they are swapped as well.
So we see that this rotation of the sphere moves a point not on this equatorial torus from one filled torus to the other. It also maps the equatorial torus to itself. This can all be done in an explicit algebraic manner using the fact that the group ![]() acts on
acts on
![]() 3) isometrically (see Vajk for details).
3) isometrically (see Vajk for details).
Now that we have all of this machinery, we can consider another curious property of
![]() , the Hopf fibration. First we will consider a fibration on
, the Hopf fibration. First we will consider a fibration on
![]() , and then examine what it looks like when this fibration is extended to the Clifford Tori.
, and then examine what it looks like when this fibration is extended to the Clifford Tori.
We can think of the
![]() as a square, or
as a square, or ![]() , with edges identified. Each pair of parallel and identified edges becomes one of the generators. First, draw a diagonal from one corner to it's opposite. Now, draw a series of lines parallel to that diagonal.
, with edges identified. Each pair of parallel and identified edges becomes one of the generators. First, draw a diagonal from one corner to it's opposite. Now, draw a series of lines parallel to that diagonal.

Now consider what these lines become when the square is wrapped up into a torus. They become a series of circles, each one circling the torus exactly once in the direction of one generator, and once in the direction of the other generator. Notice that the circles are linked, each one passing through each other one.
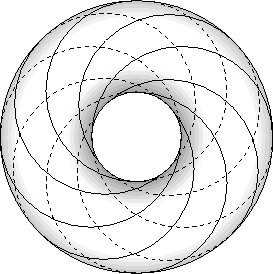
Now, consider if each of the Clifford Tori had this fibration on them. This is the Hopf Fibration. As the tubular neighborhood of these centerlines is shrunk, the tori get smaller, and the linked circles more closely approximate one of the centerlines.
In light of our knowledge of other general processes in
![]() , it now makes sense to ask whether the Clifford Tori and the Hopf Fibration can be generalized into arbitrary dimension. To answer this we need to ask what is special about the Clifford Tori that creates this symmetric division. The special characteristic seems to be the two centerlines, the circles in the x-y and z-w planes.
, it now makes sense to ask whether the Clifford Tori and the Hopf Fibration can be generalized into arbitrary dimension. To answer this we need to ask what is special about the Clifford Tori that creates this symmetric division. The special characteristic seems to be the two centerlines, the circles in the x-y and z-w planes.
The generalization of the Clifford Tori to arbitrary dimension looks like this. Inside
![]() , draw a unit circle, say in the x-y plane. Then draw a
, draw a unit circle, say in the x-y plane. Then draw a
![]() in the remaining subspace of
in the remaining subspace of
![]() where
where ![]() . For
. For
![]() , this turns out to be
, this turns out to be
![]() , consisting of just two points, the north pole and the south pole. In
, consisting of just two points, the north pole and the south pole. In
![]() , it is another unit circle in the z-w plane. And in
, it is another unit circle in the z-w plane. And in
![]() it is a sphere.
it is a sphere.
Now we can draw a surface inside the
![]() , by making a tubular neighborhood at a distance of
, by making a tubular neighborhood at a distance of
![]() around either our unit circle, or the
around either our unit circle, or the
![]() . What do these regions look like when filled? Well, the region around the unit circle is
. What do these regions look like when filled? Well, the region around the unit circle is
![]() . And the tubular neighborhood around
. And the tubular neighborhood around
![]() is
is
![]() . Only in
. Only in
![]() , when
, when ![]() , are the two regions the same.
, are the two regions the same.
So the Clifford Tori can be generalized to all spheres, but only in
![]() are they symmetric. It is not clear how the Hopf Fibration could be extended to the arbitrary dimension, as it relies on the two centerlines being the same manifold, which only happens in
are they symmetric. It is not clear how the Hopf Fibration could be extended to the arbitrary dimension, as it relies on the two centerlines being the same manifold, which only happens in
![]() . In addition, we have found another surface which divides
. In addition, we have found another surface which divides
![]() , that is,
, that is,
![]() . But only in
. But only in
![]() does this manifold divide the sphere into two identical pieces, so the Clifford Tori and the Hopf Fibration are special properties of
does this manifold divide the sphere into two identical pieces, so the Clifford Tori and the Hopf Fibration are special properties of
![]() .
.