♟ ♟ ♟
Three Player Chess Variants
Three-player games lie directly between the brutal simplicity of two-player games, and the complex, shifting allegiances of four, five, or more player games. With three players any allegiance is by definition unstable; as soon as one player is sufficiently weakened or eliminated, the allegiance shifts.
This is a quick overview of a few different variations on three-player chess, along with what makes them most interesting.
Each of the boards is available for downloading as an SVG, licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
You can also order a print of some of the more interesting boards as posters from my RedBubble store. To best match the size of normal chess boards, they should be printed at the largest size, A0, also known as 46.9″×33.0″ and cut out. RedBubble’s posters are printed on waterproof plastic, so these should hold up pretty well as game boards.
♞ ♞ ♞
General issues
Before we look at the different game boards, here’s an overview of some of the ways in which three player chess differs from two player chess.
Trading pieces
In ordinary chess, players are quite willing to capture an opponent’s piece only to lose the capturing piece immediately afterwards. In ordinary chess, this simplifies the game but does not upset the balance of power. But in three-player chess, a simple trade benefits the third player, the one who is uninvolved in the trade.
Check & checkmate
There’s really no such thing as checkmate in three player chess. This is because there are always two moves between the move that places a player’s king in “checkmate” and the point when the checkmating player could actually capture the checkmated king. So there’s always a chance for the third player to interfere with the checkmater.
Similarly, there’s always a chance for the third player to move the pieces in a way as to allow one other player to threater the other player’s king.
For these reasons, some of the three player variants stipulate that a checkmated player’s pieces become immobile when checkmated, and the checkmated king must actually be removed from the board by the attacking player when their turn comes again.
If a checkmated king were left on the board while the remaining two players play, that opens up the possibility that a subsequent move could actually bring the checkmated player back into the game. This would cripple the checkmating player; the pieces used to set up the first checkmate must be defended, and cannot move (or which must be replaceed with othe pieces in a way that maintains the checkmate).
Scoring
There are a few ways to score a three player game; the last player standing could be counted as the winner, and the two other players counted as a loss; each player could get a point for the number of kings they can capture, which allows for the possibility of a draw; or perhaps the first king to be captured counts for one point and the second counts for two.
♝ ♝ ♝
A note about ordinary chess
Ordinary chess is played on a eight-by-eight square board consisting of sixty-four square cells. This board has what mathematicians call Euclidean geometry; it’s “flat”. Some of the other boards we will be looking at have quite different topological characteristics; in layman’s terms, they are not “flat”.

♜ ♜ ♜
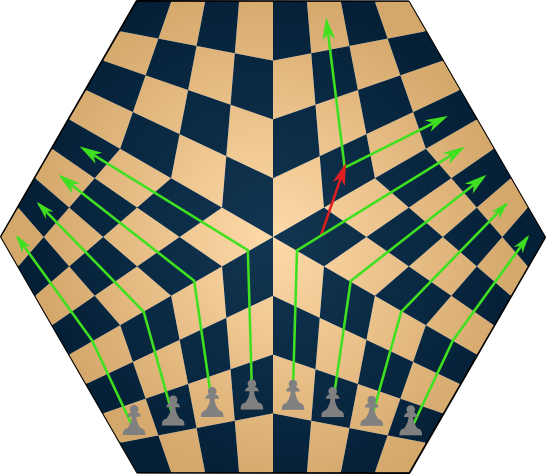
A hexagonal Euclidean grid
There have been many attempts to generalize chess to a hexagonal grid; the most popular are Gliński’s and McCooey’s. Both can be generalized to three player games on a hexagonal grid. McCooey’s variant is probably slightly better as the starting position is more compact; that game is called Echexs or Hexagonal Chess for three.

With ninety-one hexagonal cells arranged in a hexagon, this board also has a flat, Euclidean geometry. Certain pieces can move in more directions because a hexagon has more neighbors. Rooks and bishops can move in six directions, and queens and kings in twelve, and knights can reach a maximum of twelve different cells.
In order to maintain the rule that pawns move only forward, the pieces must start in a corner, rather than along an edge. In Gliński’s starting positions, there are nine pawns, and in McCooey’s, seven.
Since the board has three colors, each player gets three bishops, not two. And because a diagonal path takes a piece to hexagons that don’t even touch at a corner, diagonal moves cannot always be blocked by a line of pieces, which means that, like knights in ordinary chess, bishops, queens and even kings can sometimes jump over other pieces.
There’s an in-depth discussion of how chess pieces move on a hexagonal grid here and here.
♛ ♛ ♛
A triangular Euclidean grid
This triangular board was sold by the Noris board game company under the name Noris Schach. It consists of one hundred and six triangles in alternating colors; the pieces start lined up in a protected region. There are nine pawns and a “Cardinal”, which “moves like a queen but cannot capture and can only be captured under narrowly defined circumstances”.

This is the last of our Euclidean, “flat” boards. No distortion is necessary to fit six triangles around a point in Euclidean geometry.
Although this game was patented and sold, it’s hard to imagine exactly how the pieces move. This is because passing into a cell and out again in the same direction by definition means entering on a corner and exiting on a side, or vice versa.
This means a bishop-like diagonal move actually takes the player out the corner of the cell to a cell of the same color, and then, if it continues along the same line, out the edge of the cell to a cell of the other color. This is decidely un-bishop-like.
The knight’s and rook’s moves are obvious, but it’s not clear how to translate the rules that a pawn must always move forward and capture diagonally to a triangular grid.
♚ ♚ ♚
Two hyperbolic boards
Next up are two boards with threefold symmetry, with six regions of sixteen quadrilateral cells, for a total of ninety-six cells. I’m putting these together because they’re topologically identical—that is, one can be distorted into the other without tearing or gluing. Click here to see animation of this transformation.


These two boards have a hyperbolic, rather than Euclidean, geometry. You can see this at the centerpoint, where six cells fit around a point. It isn’t possible to put six squares around a point in Euclidean geometry, which is why the cells here have to be stretched into rhombuses. However, in hyperbolic geometry, it is possible to fit six squares around a point without distorting them.
The pieces begin arranged along three sides as in ordinary chess. On the hexagonal board, either everyone starts as if they were white, with the queen on the white cell to the left of center, or the board is rotated 60° and everyone starts as if they were black, with the queen on the black cell to the left. On the Y-shaped board, everyone must start as if they were white; a mirror image of the board would be needed for everyone to start as if they were black.
The hexagonal board also allows for two player games, where the two players begin opposite each other, with pieces arranged as in ordinary chess.
In a sense, in hyperbolic space, there are more directions to move in. You can see this on this board by considering legal moves from one of the six center cells. A bishop in that position can travel in five directions, as opposed to four on a normal chessboard; and a queen or king, nine, not eight.
A knight on one of the six center cells can reach 10 squares, two in each of the six quadrants, except for the quadrant directly opposite, which it cannot reach. (If it could, it would end up on squares of the same color, which is not possible for knights in ordinary chess.)

Because the pawns move only forward, the third of the board opposite their starting row is only reachable if the pawns move into it via a diagonal capture move. Once a pawn does move into that third of the board, they should continue in the same direction, in order to be able to reach the back row and be promoted. However, if you’re playing a two-player game on the hexagonal board, then the pawn should change direction in order to be able to reach the back row and be promoted. This means that the two-player game on the hexagonal board has the strange property that a pawn must move into the the opposite third of the board by capturing a piece in order to be promoted, which would make promotion more difficult and less common.
Although the topology of these two boards is equivalent, the hexagonally shaped board is superior, because it allows two player games and three player games starting as black in addition to starting as white.
The Y-shaped board is known as Chess for Three, and the hexagonal one as Three Player Chess. (There’s also a third board with the same underlying topology, Trichess, but it’s so ugly I didn’t want to draw it.)
♛ ♛ ♛
A spherical board
Next up is the inaccurately named “Hyperbolic Chess” board. This board has three eight by three regions, which warp together in a triangular region consisting of forty-eight quadrilateral cells. At the center are three cells arranged around a point. This means two things. First, that the board has to be colored with three colors, since there would be no way to color these three cells with two colors without having two cells of the same color next to each other here at the center. Second, it means that the board actually has spherical, rather than hyberbolic or Euclidean geometry, because only on a sphere can three squares meet at a point.

The rules for “Hyperbolic” chess were written up by Chris Lynd and are available here.
In spherical geometry, we would expect that pieces have fewer directions to move in than on the Euclidean board, and this is in fact the case. A queen or bishop on one of the three center cells has only three diagonals available to it. And a queen or a rook in the center region, while they still retain four laterals, two of them follow paralell, and, if at the center, adjacent, rows.
Since diagonals sometimes change color in the middle triangular region, this means that bishops can change color, and cover the whole board. This may not really make them more valuable, though, since the moves needed to change color are very limited.
Oddly enough, a knight on one of the center three cells has ten, not eight, cells to move to, and one “square” away from the center, it can move to nine.
Lynd’s rules for pawn movement have them able to move “forward” in two directions once they enter the central triangular region: towards the home row of either opponent.
Alternatively, pawns on the left could be forced to “orbit” the center and move towards tho home row of the opponent on the right, and vice versa. This would be similar to the pawn movement of the true hyperbolic boards above, where four pawns move towards the home row of each opponent. This would mean that each pawn starts off thirteen cells away from promotion, as opposed to seven, which would make promotion more difficult and less common.
♜ ♜ ♜
A circular board
This may be one of the most interesting three player chess boards out there. It’s a circular board with quadrilateral cells, twenty-four cells in circumference, and six cells deep, for a total of one hundred and forty-four cells. In the middle of the board, there is circular zone where pieces cannot land, but through which pieces can pass, laterally directly across, and diagonally following a spiral.

It is this spiral diagonal move which makes this board interesting. When following this spiral, a piece ends up not on the cell of the same color directly opposite the board, but the next cell of the same color to the left of the one directly opposite, if it’s moving diagonally to the right; and on the next cell of the same color to the right of the one directly opposite, if it’s moving diagonally to the left. This has an interesting property: an unobstructed bishop or queen’s path runs from the outer edge, diagonally to the left or the right, and through the center and back to the same cell on the outer edge.
Since the cell a piece ends up on when that piece crosses through the center depends not only on where the piece left the inner edge but what kind of movement it was making, that means that the topology of this board is not simple. Without this diagonal move rule, it might be topologically equivalent to the projective plane or cross-cap.
This board also has “moats” and “creeks”. According to the official rules, moats extend one cell up from the outer edge and cannot be crossed. This prevents, for example, neighboring rooks from capturing each other on the first move. Once a team is eliminated or has vacated the outer rank, then the moat is considerd “bridged” and can be crossed.
Continuing on from the moats for two more cells are the creeks. Creeks only affect pawns, which cannot capture across creeks until they have crossed through the center.
This board is available from Vat19 as Three Man Chess.
♝ ♝ ♝
A revised circular board
I was curious how hard it would be to create a circular board where the diagonal paths crossed directly across the center, and whether it would be possible to remove the odd moats and creeks of the above design. This is the result. The three players start as before, along the outer edge. It’s thirty cells around, by eight cells deep, with six missing cells along the outer edge, for a total of 234 cells.
The six missing cells eliminate the need for moats, as rooks cannot threaten each other at the start of the game. The extra two cells added between the starting cells eliminates the need for creeks, as pawns cannot interfere with their neighbors as soon as they start moving; they would need some pieces to capture before they can get far enough over to interfere.
Making the board eight cells deep preserves the property that a bishop or a queen can move back towards the outer row or through the center and threaten the same cell on the outer row, but also adds another property; that a bishop or queen passes directly across the board when passing through the center, and also effectively flips the diagonal direction that it’s traveling in. This makes it easier to determine where a bishop is going to land upon crossing the center; unlike on the other board, where a bishop crosses to a cell a few cells off from directly opposite, bishops on this board cross directly across and continue moving diagonally.

The simpler behavior of diagonally moving pieces makes the topology of this center of this board equivalent to that of the projective plane or cross-cap. And, since this board has a single outer edge, it’s actually topologically equivalent to the Möbius strip.
♞ ♞ ♞
Conclusion
That’s all! Hopefully you have enjoyed this journey into chess game play, chess rules, geometry, and topology.
