Lobeck's account of NP Ellipsis

Lobeck (1995) takes an in-depth look at NP Ellipsis, and argues that it can be integrated into a larger framework including VP Ellipsis and Sluicing. I will briefly summarize her arguments here, and show why an account in terms of Merchant's identity condition is more complete.

First, Lobeck argues, unconvincingly I think, that all VP ellipsis, NP ellipsis, and Sluicing can be pragmatically controlled (p. 25). This claim includes those cases that Hankamer & Sag argue must be syntactically controlled. She argues this point on the basis of non-declarative sentences with VP Ellipsis which appear to be pragmatically controlled, the sort of super-salience mentioned in section 3, a point which Hankamer & Sag acknowledge. However, the distinction between pragmatically controlled and syntactically controlled ellipsis is robust enough that it should be accounted for, regardless of whether or not it is a universal, black-and-white process.

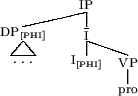
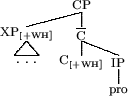
Next, Lobeck argues that all three kinds of ellipsis sites are filled with a silent pro, which is present from deep structure, and interpreted either at surface structure, or at LF. Finally, she argues that this pro must be properly governed by a head which exhibits strong agreement features.

Lobeck argues that it makes more sense to assume that these ellipsis sites are filled with a pro than deleted, because deletion is an operation at PF, interpretation of ellipsis sites is an operation at LF, and these levels have no access to each other. However, this is exactly the problem addressed by Merchant (1999), and as I have already shown, the identity condition developed there works for NP Ellipsis.

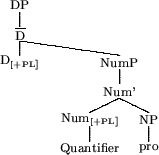
The structures that Lobeck predicts to be acceptable ellipsis structures are the following, where [+WH], [+PLURAL], [+POSSESSIVE], and [PHI] are the ``strong agreement features'' which can properly head govern the silent pro.

VP Ellipsis	Sluicing	NP Ellipsis	NP Ellipsis

Lobeck must account for the uses of quantifiers and numbers (which in her account head NumP) without overt NPs, within her framework of strong agreement features. A theory which accounts for the pragmatic/syntactic control distinctions, does not conflate bare quantifiers with bare possessors, and accounts for the identity requirements on all three types of ellipsis with a single condition is much more empirically complete and theoretically compact.

Although there may be some merit to the generalization that agreement and this type of ellipsis are linked, any account in terms of strong agreement features will always have problems with cases of VP Ellipsis in English where multiple stacked auxiliaries precede the ellipsis site, and agreement is not realized on multiple heads;

(93) Bob wasn't talking, but Mary could have been talking.

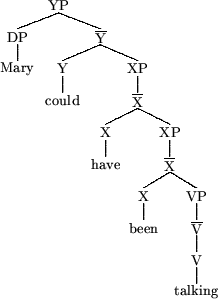
Regardless of the specific syntactic theory, if ellipsis is licensed by strong agreement features, you must locate the same strong features on both XPs and the VP above, since all three phrases are valid candidates for ellipsis. In other words, it is generally assumed that strong agreement features are located on some functional head, either I$^\circ$, or Agr$^\circ$ or T$^\circ$. But if three of the phrases above are eligible for ellipsis, then the strong agreement features which license ellipsis must be covertly located in three places instead of one, yet they only appear overtly in the topmost position.

At some point, perhaps the syntactic control facts can be unified with the observation that agreement and ellipsis are linked. But for now, it remains only an observation.