The n-dimensional sphere is the set of all points in ![]() space at a given radius from a center point. The radius is denoted by
space at a given radius from a center point. The radius is denoted by ![]() and the center by
and the center by
![]() .
.
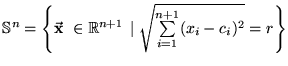
Unless otherwise stated, the center of the sphere is assumed to be
![]() and the radius is assumed to be 1. Under this definition,
and the radius is assumed to be 1. Under this definition,
![]() is the two points
is the two points
![]() in
in
![]() ,
,
![]() is the unit circle in
is the unit circle in
![]() , and
, and
![]() is the object which is commonly called the sphere or globe, in
is the object which is commonly called the sphere or globe, in
![]() .
.
An n-Disk is simply the set of all points inside
![]() , or all points less than or equal to
, or all points less than or equal to ![]() units away from the center
units away from the center
![]() .
.
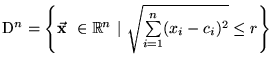
Under this definition, the 1-disk is the line segment between ![]() and
and ![]() on
on
![]() , the 2-disk is the interior of the circle of radius
, the 2-disk is the interior of the circle of radius ![]() in
in
![]() , and the 3-disk or 3-ball is the interior of the sphere of radius
, and the 3-disk or 3-ball is the interior of the sphere of radius ![]() in
in
![]() . As above, the center is assumed to be
. As above, the center is assumed to be
![]() and the radius to be 1 unless otherwise specified.
and the radius to be 1 unless otherwise specified.
Throughout this paper I will use the term manifold in its standard topological sense. A n-dimensional manifold is usually defined as a set with a collection of patches, or 1-1 functions from
![]() , where
, where ![]() is an open subset of
is an open subset of
![]() , such that the following two conditions are satisfied:
, such that the following two conditions are satisfied:
(i.) The images of the patches cover ![]()
(ii.) For two patches ![]() and
and ![]() , the composition
, the composition
![]() and
and
![]() are differentiable and defined on open sets in
are differentiable and defined on open sets in
![]() (O'Neill).
(O'Neill).
The ![]() operator is the Cartesian product. It takes two manifolds of dimension
operator is the Cartesian product. It takes two manifolds of dimension ![]() and
and ![]() , and duplicates the one at every point along the other, creating a manifold of dimension
, and duplicates the one at every point along the other, creating a manifold of dimension ![]() .
.
A generator is a manifold ![]() contained in another manifold
contained in another manifold ![]() such that
such that ![]() crossed with some other manifold
crossed with some other manifold ![]() makes
makes ![]() . In other words, if
. In other words, if
![]() , then
, then ![]() and
and ![]() are generators of
are generators of ![]() . For example, since
. For example, since
![]() , the generators of
, the generators of
![]() are the two
are the two
![]() .
.
An equator inside
![]() is a
is a
![]() . This can be seen by setting one of the coordinates, say
. This can be seen by setting one of the coordinates, say ![]() , to zero, and taking all remaining points in
, to zero, and taking all remaining points in
![]() .
.
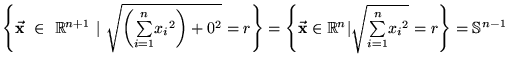
It's fairly trivial to see that two line segments, each end of one segment joined to an end of the other segment, make a circle (or something that can be deformed into a circle). However, the process generalizes to all dimensions, and provides us with a technique of visualizing
![]() .
.
Two 2-disks, or filled circles, can be joined along their circular boundaries, to make
![]() . Each disk makes a hemisphere, and the boundary between the two becomes the equator.
. Each disk makes a hemisphere, and the boundary between the two becomes the equator.
In general, an equator as defined above is
![]() in
in
![]() . Now, all the other points in
. Now, all the other points in
![]() are the points where
are the points where ![]() . So the other points in
. So the other points in
![]() are split into two groups:
are split into two groups: ![]() and
and ![]() . We can see that these two sets of points are N-disks because we can let
. We can see that these two sets of points are N-disks because we can let ![]() range from 1 to 0, and get a corresponding
range from 1 to 0, and get a corresponding
![]() for each value of
for each value of ![]() .
.